内存分段

威斯康辛州大学操作系统书籍《Operating Systems: Three Easy Pieces》读书笔记系列之 Virtualization（虚拟化）。本篇为虚拟化技术的基础篇系列第三篇（Memory Virtualization），内存虚拟化。内存虚拟化又将分为两篇，本篇为第二篇内存虚拟化之基础 - 内存分段和空闲空间管理

Segmentation

• 如果我们将整个地址空间放入物理内存，那么栈和堆之间的空间并没有被进程使用，却依然占用了实际的物理内存。因此，简单的通过基址寄存器和界限寄存器实现的虚拟内存很浪费。另外，如果剩余物理内存无法提供连续区域来放置完整的地址空间，进程便无法运行。这种基址加界限的方式看来并不像我们期望的那样灵活。

• CRUX：怎样支持大地址空间？

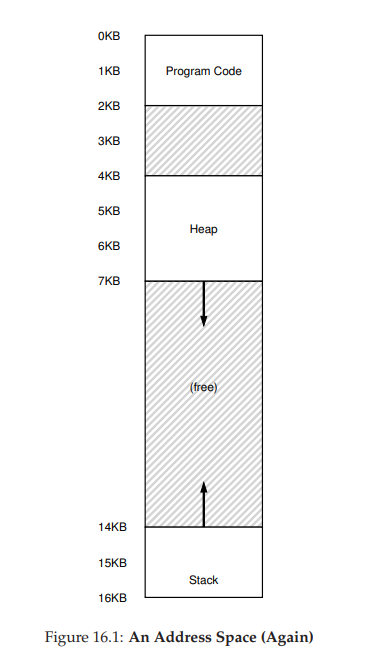
Segmentation: Generalized Base/Bounds

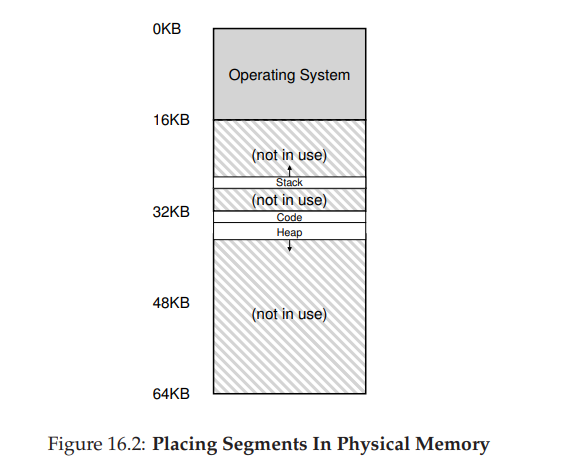
• 在 MMU 中引入不止一个基址和界限寄存器对，而是给地址空间内的每个逻辑段（segment）一对。一个段只是地址空间里的一个连续定长的区域，在典型的地址空间里有 3 个逻辑不同的段：代码、栈和堆。分段的机制使得操作系统能够将不同的段放到不同的物理内存区域，从而避免了虚拟地址空间中的未使用部分占用物理内存。

• 如图所示，64KB 的物理内存除去操作系统占用的 16KB 内存外可以划分成三个段，给每个段都分配一对基址和界限寄存器。

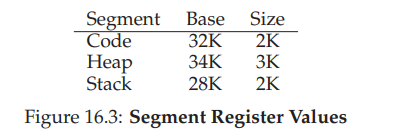
• 下表记录了上图例中的寄存器值，每个界限寄存器记录了一个段的大小。

• 地址转换举例：
• 假设现在要引用虚拟地址 100（在代码段中），MMU 将基址值加上偏移量（100）得到实际的物理地址：100 + 32KB = 32868。然后它会检查该地址是否在界限内（100 小于 2KB），发现是的，于是发起对物理地址 32868 的引用。
• 一个堆中的地址，虚拟地址 4200。（参考图16.1） 如果用虚拟地址 4200 加上堆的基址（34KB），得到物理地址 39016，这不是正确的地址。我们首先应该先减去地址空间中堆的偏移量，即该地址指的是这个段中的哪个字节。因为堆从虚拟地址 4K（4096）开始，4200 的偏移量实际上是 4200 减去 4096，即 104，然后用这个偏移量（104）加上基址寄存器中的物理地址（34KB），得到真正的物理地址 34920。

• 如果我们试图访问非法的地址，例如 7KB，超出了堆的边界呢。硬件会发现该地址越界，因此陷入操作系统，很可能导致终止出错进程。从而产生段异常（segmentation violation）或段错误（segmentation fault）。

Which Segment Are We Referring To?

• 硬件在地址转换时使用段寄存器。它如何知道段内的偏移量，以及地址引用了哪个段？

Explicit

• 一种常见的方式，有时称为显式（explicit）方式，就是用虚拟地址的开头几位来标识不同的段，VAX/VMS 系统使用了这种技术。上述例子中有三个段，相应的需要两位就可以表示了。如果我们用 14 位虚拟地址的前两位来标识，那么前两位即为对应的段号，后12位则为偏移量。上述的 4200 （堆段+104）就标识为 01 0000 0110 1000
• 00 代码段 01 堆段 11 栈段（因为起始地址为 00 0000 0000 0000，地址空间如图所示 0-2KB 为代码段，二进制表示前四位为 0000-0010，4KB 为堆的起始地址，二进制表示前四位为 0100）

• 偏移量简化了对段边界的判断。我们只要检查偏移量是否小于界限，大于界限的为非法地址。因此，如果基址和界限放在数组中（每个段一项），为了获得需要的物理地址，硬件会做下面这样的事：在上述 14 位虚拟地址的例子中，对应 SEG_MASK 即为 0x3000，SEG_SHIFT 为 12，OFFSET_MASK 为 0xFFF。

• 由于用了两位来表示段号，但其实是可以表述四个段的，浪费了一个表示，所以有些系统会将堆和栈放在一个段中，因此就只需要一位来表示。

Implict

• 隐式（implicit）方式中，硬件通过地址产生的方式来确定段。

• 例如，如果地址由程序计数器产生（即它是指令获取），那么地址在代码段。如果基于栈或基址指针，它一定在栈段。其他地址则在堆段。

What About The Stack?

• 上述例子中未涉及到栈的地址转换。在表 16.3 中，栈被重定位到物理地址 28KB。但有一点关键区别，它 反向增长。物理内存中，它始于 28KB，增长回到 26KB，相应虚拟地址从 16KB 到 14KB。因此地址转换方式和其他段会有所不同。

• 所以对于段的硬件支持除了基地址寄存器和界限寄存器以外，还需要知道段地址的增长方向，可以用一位来表示。更新后的寄存器结果如下：1 表示正向增长（从小到大），0 表示反向增长。

• 假设要访问虚拟地址 15KB，根据图 16.1 知道这是个栈地址，以及根据物理内存的对应关系不难发现物理地址为 27KB。虚拟地址的二进制形式为 11 1100 0000 0000，前两位表示为 stack 段，偏移量为 3KB，但此时非正确偏移，只是二进制地址表示中的地址偏移。为了得到正确的反向偏移，我们必须从 3KB 中减去最大的段地址：在这个例子中，段可以是 4KB，因此正确的偏移量是 3KB 减去 4KB，即−1KB。只要用这个反向偏移量（−1KB）加上基址（28KB），就得到了正确的物理地址 27KB。用户可以进行界限检查，确保反向偏移量的绝对值小于段的大小。

Support for Sharing

• 随着分段机制的不断改进，系统设计人员很快意识到，通过再多一点的硬件支持，就能实现新的效率提升。具体来说，要节省内存，有时候在地址空间之间共享（share）某些内存段是有用的。尤其是，代码共享很常见，今天的系统仍然在使用。

• 为了支持共享，需要一些额外的硬件支持，这就是保护位（protection bit）。基本为每个段增加了几个位，标识程序是否能够读写该段，或执行其中的代码。通过将代码段标记为只读，同样的代码可以被多个进程共享，而不用担心破坏隔离。虽然每个进程都认为自己独占这块内存，但操作系统秘密地共享了内存，进程不能修改这些内存，所以假象得以保持。

• 如下表所示。代码段的权限是可读和可执行，因此物理内存中的一个段可以映射到多个虚拟地址空间。有了保护位，前面描述的硬件算法也必须改变。除了检查虚拟地址是否越界，硬件还需要检查特定访问是否允许。如果用户进程试图写入只读段，或从非执行段执行指令，硬件会触发异常，让操作系统来处理出错进程。

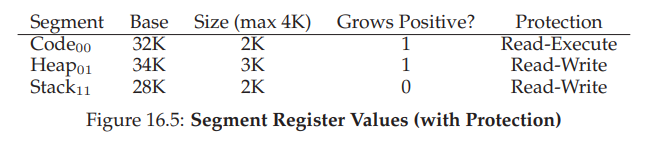
Fine-grained vs. Coarse-grained Segmentation

• 到目前为止，我们的例子大多针对只有很少的几个段的系统（即代码、栈、堆）。我们可以认为这种分段是粗粒度的（coarse-grained），因为它将地址空间分成较大的、粗粒度的块。但是，一些早期系统更灵活，允许将地址空间划分为大量较小的段，这被称为细粒度（fine-grained）分段。

• 支持许多段需要进一步的硬件支持，并在内存中保存某种段表（segment table）。这种段表通常支持创建非常多的段，因此系统使用段的方式，可以比之前讨论的方式更灵活。例如，像 Burroughs B5000 这样的早期机器可以支持成千上万的段，有了操作系统和硬件的支持，编译器可以将代码段和数据段划分为许多不同的部分。当时的考虑是，通过更细粒度的段，操作系统可以更好地了解哪些段在使用哪些没有，从而可以更高效地利用内存。

OS Support

• 系统运行时，地址空间中的不同段被重定位到物理内存中。与我们之前介绍的整个地址空间只有一个基址/界限寄存器对的方式相比，大量节省了物理内存。具体来说，栈和堆之间没有使用的区域就不需要再分配物理内存，让我们能将更多地址空间放进物理内存。

• 分段也带来了一些新的问题：
• 操作系统在上下文切换时应该做什么？各个段寄存器中的内容必须保存和恢复。显然，每个进程都有自己独立的虚拟地址空间，操作系统必须在进程运行前，确保这些寄存器被正确地赋值。
• 管理物理内存的空闲空间。新的地址空间被创建时，操作系统需要在物理内存中为它的段找到空间。之前，我们假设所有的地址空间大小相同，物理内存可以被认为是一些槽块，进程可以放进去。现在，每个进程都有一些段，每个段的大小也可能不同。一般会遇到的问题是，物理内存很快充满了许多空闲空间的小洞，因而很难分配给新的段，或扩大已有的段。这种问题被称为外部碎片

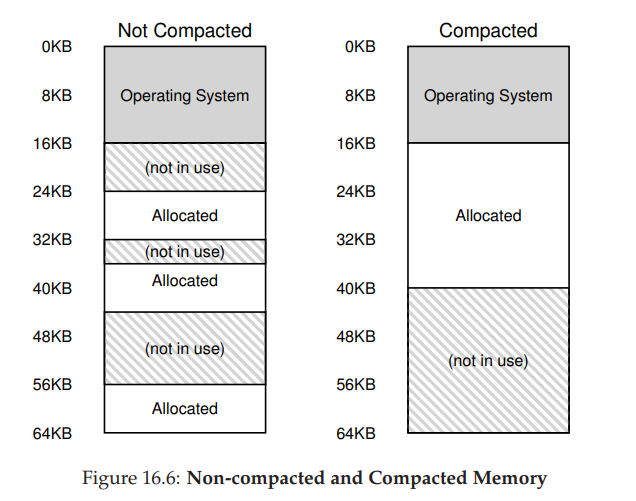
• 在这个例子中，一个进程需要分配一个 20KB 的段。当前有 24KB 空闲，但并不连续（是3 个不相邻的块）。因此，操作系统无法满足这个 20KB 的请求。该问题的一种解决方案是紧凑（compact）物理内存，重新安排原有的段。例如，操作系统先终止运行的进程，将它们的数据复制到连续的内存区域中去，改变它们的段寄存器中的值，指向新的物理地址，从而得到了足够大的连续空闲空间。这样做，操作系统能让新的内存分配请求成功。但是，内存紧凑 Compact 成本很高，因为拷贝段是内存密集型的，一般会占用大量的处理器时间。

• 一种更简单的做法是利用空闲列表管理算法，试图保留大的内存块用于分配。相关的算法可能有成百上千种，包括传统的最优匹配（best-fit，从空闲链表中找最接近需要分配空间的空闲块返回）、最坏匹配（worst-fit）、首次匹配（first-fit）以及像伙伴算法（buddy algorithm）这样更复杂的算法。

• 无论算法多么精妙，都无法完全消除外部碎片，因此，好的算法只是试图减小它。

Summary

• 分段解决了一些问题，帮助我们实现了更高效的虚拟内存。不只是动态重定位，通过避免地址空间的逻辑段之间的大量潜在的内存浪费，分段能更好地支持稀疏地址空间。它还很快，因为分段要求的算法很容易，很适合硬件完成，地址转换的开销极小。分段还有一个附加的好处：代码共享。如果代码放在独立的段中，这样的段就可能被多个运行的程序共享。

• 但我们已经知道，在内存中分配不同大小的段会导致一些问题，我们希望克服。首先，是我们上面讨论的外部碎片。由于段的大小不同，空闲内存被割裂成各种奇怪的大小，因此满足内存分配请求可能会很难。用户可以尝试采用聪明的算法，或定期紧凑内存，但问题很根本，难以避免。

• 第二个问题也许更重要，分段还是不足以支持更一般化的稀疏地址空间。例如，如果有一个很大但是稀疏的堆，都在一个逻辑段中，整个堆仍然必须完整地加载到内存中。换言之，如果使用地址空间的方式不能很好地匹配底层分段的设计目标，分段就不能很好地工作。因此我们需要找到新的解决方案。

Free-Space Management

• 如果要管理的空闲空间由大小不同的单元构成，管理就变得困难（而且有趣）。这种情况出现在用户级的内存分配库（如 malloc() 和 free()），或者操作系统用分段（segmentation）的方式实现虚拟内存。在这两种情况下，出现了外部碎片（external fragmentation）的问题：空闲空间被分割成不同大小的小块，成为碎片，后续的请求可能失败，因为没有一块足够大的连续空闲空间，即使这时总的空闲空间超出了请求的大小。

• CRUX：要满足变长的分配请求，应该如何管理空闲空间？什么策略可以让碎片最小化？不同方法的时间和空间开销如何？

Assumptions

• 假定基本的接口就像 malloc() 和 free()提供的那样。具体来说，void * malloc(size tsize)需要一个参数 size，它是应用程序请求的字节数。函数返回一个指针（没有具体的类型，在 C 语言的术语中是 void 类型），指向这样大小（或较大一点）的一块空间。对应的函数 void free(void *ptr) 函数接受一个指针，释放对应的内存块。请注意该接口的隐含意义，在释放空间时，用户不需告知库这块空间的大小。因此，在只传入一个指针的情况下，库必须能够弄清楚这块内存的大小。

• 进一步假设，我们主要关心的是外部碎片（external fragmentation），如上所述。当然，分配程序也可能有内部碎片（internal fragmentation）的问题。如果分配程序给出的内存块超出请求的大小，在这种块中超出请求的空间（因此而未使用）就被认为是内部碎片（因为浪费发生在已分配单元的内部），这是另一种形式的空间浪费。但是，简单起见，这里主要讨论外部碎片。

• 还假设，内存一旦被分配给客户，就不可以被重定位到其他位置。例如，一个程序调用 malloc()，并获得一个指向堆中一块空间的指针，这块区域就“属于”这个程序了，库不再能够移动，直到程序调用相应的 free() 函数将它归还。因此，不可能进行压缩（compaction）空闲空间的操作，从而减少碎片。但是，操作系统层在实现分段（segmentation）时，却可以通过压缩来减少碎片。

• 最后我们假设，分配程序所管理的是连续的一块字节区域。在一些情况下，分配程序可以要求这块区域增长。例如，一个用户级的内存分配库在空间快用完时，可以向内核申请增加堆空间（通过 sbrk 这样的系统调用），但是，简单起见，我们假设这块区域在整个生命周期内大小固定。

Low-level Mechanisms

Splitting and Coalescing

• 空闲列表包含一组元素，记录了堆中的哪些空间还没有分配。假设有下面的 30 字节的堆：

• 这个堆对应的空闲列表会有两个元素，一个描述第一个 10 字节的空闲区域（字节0～9），一个描述另一个空闲区域（字节 20～29）：

• 任何大于 10 字节的分配请求都会失败（返回 NULL），因为没有足够的连续可用空间。而恰好 10 字节的需求可以由两个空闲块中的任何一个满足。但是，如果申请小于 10 字节空间，分配程序会执行所谓的 分割（splitting）动作：它找到一块可以满足请求的空闲空间，将其分割，第一块返回给用户，第二块留在空闲列表中。

• 假设分配 1 字节，分配程序选择使用第二块空闲空间，对 malloc()的调用会返回 20（1 字节分配区域的地址），空闲列表会变成这样：

• 许多分配程序中因此也有一种机制，名为合并（coalescing）。还是看前面的例子（10字节的空闲空间，10 字节的已分配空间，和另外 10 字节的空闲空间）。

• 对于这个（小）堆，如果应用程序调用 free(10)，归还堆中间的空间，会发生什么？如果只是简单地将这块空闲空间加入空闲列表，不多想想，可能得到如下的结果：

• 问题出现了：尽管整个堆现在完全空闲，但它似乎被分割成了 3 个 10 字节的区域。这时，如果用户请求 20 字节的空间，简单遍历空闲列表会找不到这样的空闲块，因此返回失败。

• 为了避免这个问题，分配程序会在释放一块内存时合并可用空间。想法很简单：在归还一块空闲内存时，仔细查看要归还的内存块的地址以及邻它的空闲空间块。如果新归还的空间与一个原有空闲块相邻（或两个，就像这个例子），就将它们合并为一个较大的空闲块。通过合并，最后空闲列表应该像这样：

Tracking The Size Of Allocated Regions

• free(void *ptr) 接口没有块大小的参数。因此它是假定，对于给定的指针，内存分配库可以很快确定要释放空间的大小，从而将它放回空闲列表。

• 要完成这个任务，大多数分配程序都会在头块（header）中保存一点额外的信息，它在内存中，通常就在返回的内存块之前。如下图所示的例子中，检查一个 20 字节的已分配块，由 ptr 指着，设想用户调用了 malloc()，并将结果保存在 ptr 中：ptr = malloc(20)。

• 该 head 块中至少包含所分配空间的大小（这个例子中是 20）。它也可能包含一些额外的指针来加速空间释放，包含一个幻数来提供完整性检查，以及其他信息。我们假定，一个简单的 head 块包含了分配空间的大小和一个幻数：

• 用户调用 free(ptr)时，库会通过简单的指针运算得到头块的位置：

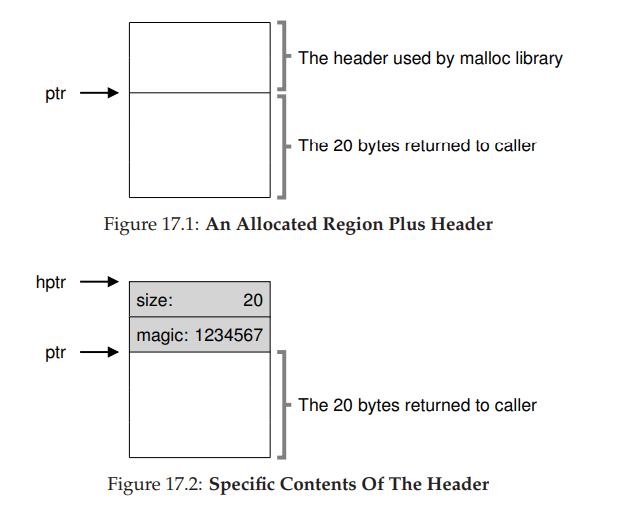
• 获得 head 块的指针后，库可以很容易地确定幻数是否符合预期的值，作为正常性检查（assert（hptr->magic == 1234567）），并简单计算要释放的空间大小即 head 块的大小加区域长度）。实际释放的是 head 块大小加上分配给用户的空间的大小。因此，如果用户请求 N 字节的内存，库不是寻找大小为 N 的空闲块，而是寻找 N 加上 head 块大小的空闲块。

Embedding A Free List

• 这个简单的空闲列表还只是一个概念上的存在，它就是一个列表，描述了堆中的空闲内存块。但如何在空闲内存自己内部建立这样一个列表呢？

• 假设我们需要管理一个 4096 字节的内存块（即堆是 4KB）。为了将它作为一个空闲空间列表来管理，首先要初始化这个列表。开始，列表中只有一个条目，记录了大小为 4096 的空间（减去 head 块的大小）。下面是该列表中一个节点描述：

• 现在来看一些代码，它们初始化堆，并将空闲列表的第一个元素放在该空间中。假设堆构建在某块空闲空间上，这块空间通过系统调用 mmap() 获得。这不是构建这种堆的唯一选择，但在这个例子中很合适。下面是代码：

• 执行这段代码之后，列表的状态是它只有一个条目，记录大小为 4088。head 指针指向这块区域的起始地址，假设是 16KB（尽管任何虚拟地址都可以）。现在，假设有一个 100 字节的内存请求。为了满足这个请求，库首先要找到一个足够大小的块。因为只有一个 4088 字节的块，所以选中这个块。然后，这个块被分割（split）为两块：一块足够满足请求（以及头块，如前所述），一块是剩余的空闲块。假设记录 head 块为 8 个字节（一个整数记录大小，一个整数记录幻数），堆中的空间如图所示。

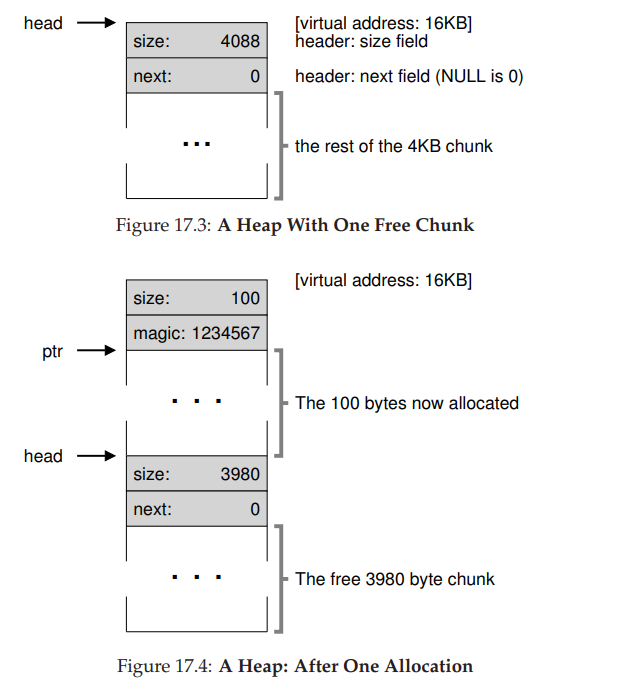
• 对于 100 字节的请求，库从原有的一个空闲块中分配了 108 字节，返回指向它的一个指针（在上图中用 ptr 表示），并在其之前连续的 8 字节中记录头块信息，供未来的 free() 函数使用。同时将列表中的空闲节点缩小为 3980 字节（4088−108）。

• 现在再来看该堆，其中有 3 个已分配区域，每个 100（加上头块是 108）。这个堆如图所示。可以看出，堆的前 324 字节已经分配，因此我们看到该空间中有 3 个头块，以及 3 个 100 字节的用户使用空间。空闲列表只有一个节点（由 head 指向），但在 3 次分割后，现在大小只有 3764 字节。

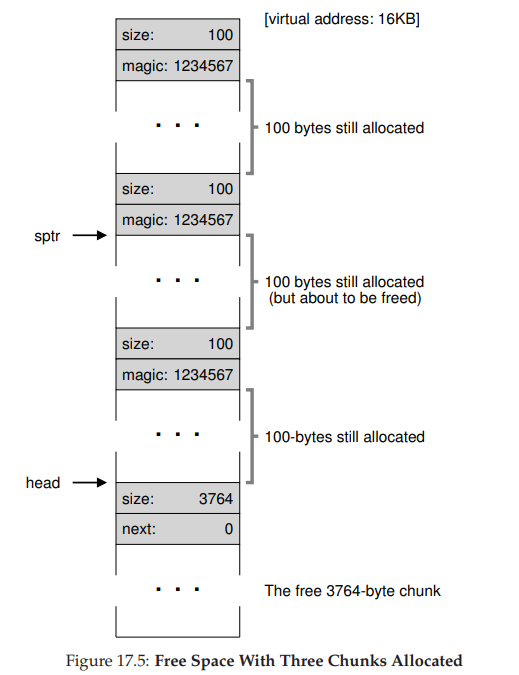
• 但如果用户程序通过 free() 归还一些内存，在这个例子中，应用程序调用 free(16500)，归还了中间的一块已分配空间（内存块的起始地址 16384 加上前一块的 108，和这一块的头块的 8 字节，就得到了 16500）。这个值在前图中用 sptr 指向。库马上弄清楚了这块要释放空间的大小，并将空闲块加回空闲列表。假设我们将它插入到空闲列表的头位置，该空间如图所示。

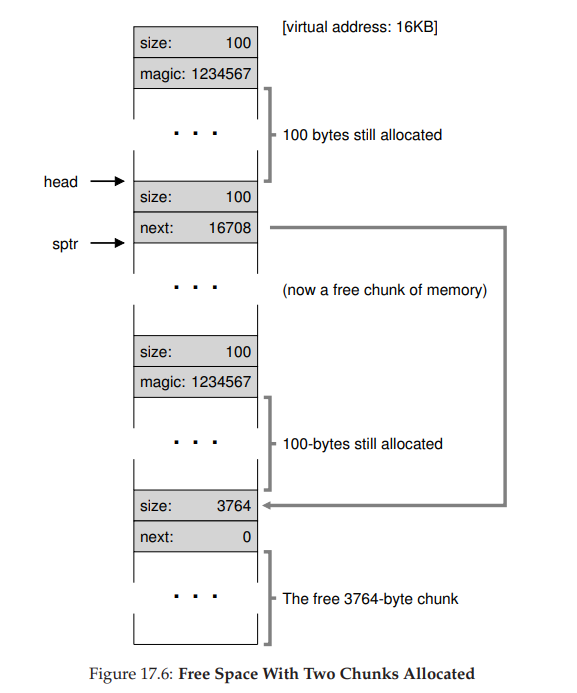
• 现在的空闲列表包括一个小空闲块（100 字节，由列表的头指向）和一个大空闲块（3764字节）。

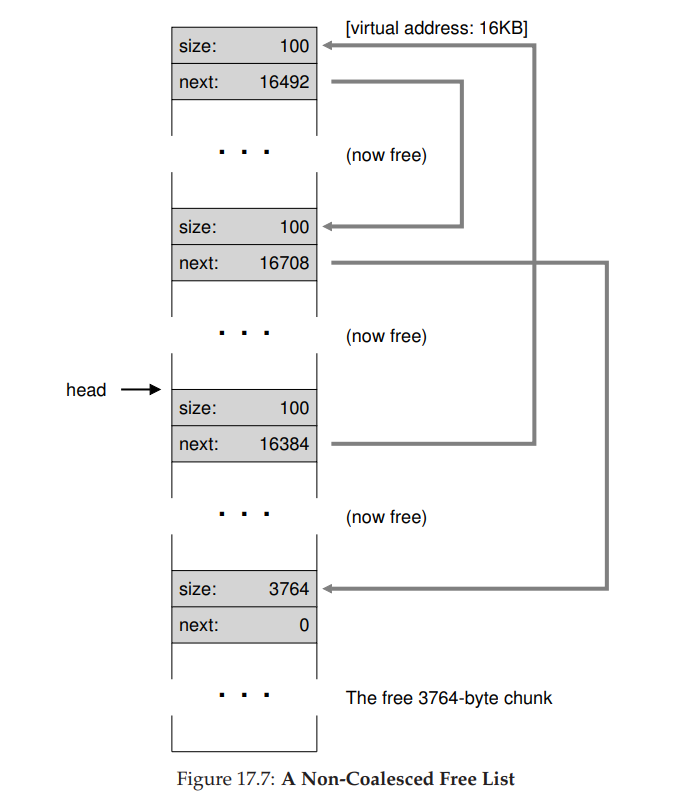
• 现在假设剩余的两块已分配的空间也被释放。没有合并，空闲列表将非常破碎，如图 17.7 所示。我们忘了合并（coalesce）列表项，虽然整个内存空间是空闲的，但却被分成了小段，因此形成了碎片化的内存空间。解决方案很简单：遍历列表，合并（merge）相邻块。完成之后，堆又成了一个整体。

Growing The Heap

• 如果堆中的内存空间耗尽，应该怎么办？最简单的方式就是返回失败。在某些情况下这也是唯一的选择，因此返回 NULL 也是一种体面的方式。

• 大多数传统的分配程序会从很小的堆开始，当空间耗尽时，再向操作系统申请更大的空间。通常，这意味着它们进行了某种系统调用（例如，大多数 UNIX 系统中的 sbrk），让堆增长。操作系统在执行 sbrk 系统调用时，会找到空闲的物理内存页，将它们映射到请求进程的地址空间中去，并返回新的堆的末尾地址。这时，就有了更大的堆，请求就可以成功满足。

Basic Strategies

• 理想的分配程序可以同时保证快速和碎片最小化。遗憾的是，由于分配及释放的请求序列是任意的（毕竟，它们由用户程序决定），任何特定的策略在某组不匹配的输入下都会变得非常差。所以我们不会描述“最好”的策略，而是介绍一些基本的选择，并讨论它们的优缺点。

Best Fit

• 最优匹配（best fit）策略非常简单：首先遍历整个空闲列表，找到和请求大小一样或更大的空闲块，然后返回这组候选者中最小的一块。这就是所谓的最优匹配（也可以称为最小匹配）。只需要遍历一次空闲列表，就足以找到正确的块并返回。

• 最优匹配背后的想法很简单：选择最接它用户请求大小的块，从而尽量避免空间浪费。然而，这有代价。简单的实现在遍历查找正确的空闲块时，要付出较高的性能代价。

Worst Fit

• 最差匹配（worst fit）方法与最优匹配相反，它尝试找最大的空闲块，分割并满足用户需求后，将剩余的块（很大）加入空闲列表。

• 最差匹配尝试在空闲列表中保留较大的块，而不是向最优匹配那样可能剩下很多难以利用的小块。但是，最差匹配同样需要遍历整个空闲列表。更糟糕的是，大多数研究表明它的表现非常差，导致过量的碎片，同时还有很高的开销。

First Fit

• 首次匹配（first fit）策略就是找到第一个足够大的块，将请求的空间返回给用户。同样，剩余的空闲空间留给后续请求。

• 首次匹配有速度优势（不需要遍历所有空闲块），但有时会让空闲列表开头的部分有很多小块。因此，分配程序如何管理空闲列表的顺序就变得很重要。
• 一种方式是基于地址排序（address-based ordering）。通过保持空闲块按内存地址有序，合并操作会很容易，从而减少了内存碎片。

Next Fit

• 不同于首次匹配每次都从列表的开始查找，下次匹配（next fit）算法多维护一个指针，指向上一次查找结束的位置。其想法是将对空闲空间的查找操作扩散到整个列表中去，避免对列表开头频繁的分割。

• 这种策略的性能与首次匹配很接近，同样避免了遍历查找。

Examples

• 设想一个空闲列表包含 3 个元素，长度依次为 10、30、20（我们暂时忽略头块和其他细节，只关注策略的操作方式）：

• 假设有一个 15 字节的内存请求。最优匹配会遍历整个空闲列表，发现 20 字节是最优匹配，因为它是满足请求的最小空闲块。结果空闲列表变为：本例中发生的情况，在最优匹配中常常发生，现在留下了一个小空闲块。

• 最差匹配类似，但会选择最大的空闲块进行分割，在本例中是 30。结果空闲列表变为：在这个例子中，首次匹配会和最差匹配一样，也发现满足请求的第一个空闲块。不同的是查找开销，最优匹配和最差匹配都需要遍历整个列表，而首次匹配只找到第一个满足需求的块即可，因此减少了查找开销。

Other Approaches

Segregated Lists

• 一直以来有一种很有趣的方式叫作分离空闲列表（segregated list）。基本想法很简单：如果某个应用程序经常申请一种（或几种）大小的内存空间，那就用一个独立的列表，只管理这样大小的对象。其他大小的请求都一给更通用的内存分配程序。

• 这种方法的好处显而易见。通过拿出一部分内存专门满足某种大小的请求，碎片就不再是问题了。而且，由于没有复杂的列表查找过程，这种特定大小的内存分配和释放都很快。

• 但也引入了新的复杂性。例如，应该拿出多少内存来专门为某种大小的请求服务，而将剩余的用来满足一般请求？超级工程师 Jeff Bonwick 为 Solaris 系统内核设计的厚块分配程序（slab allocator），很优雅地处理了这个问题

• 具体来说，在内核启动时，它为可能频繁请求的内核对象创建一些对象缓存（object cache），如锁和文件系统 inode 等。这些的对象缓存每个分离了特定大小的空闲列表，因此能够很快地响应内存请求和释放。
• 如果某个缓存中的空闲空间快耗尽时，它就向通用内存分配程序申请一些内存 slab（总量是页大小和对象大小的公倍数）。
• 相反，如果给定 slab 中对象的引用计数变为 0，通用的内存分配程序可以从专门的分配程序中回收这些空间，这通常发生在虚拟内存系统需要更多的空间的时候。

• slab 分配程序比大多数分离空闲列表做得更多，它将列表中的空闲对象保持在预初始化的状态。Bonwick 指出，数据结构的初始化和销毁的开销很大。通过将空闲对象保持在初始化状态，slab 分配程序避免了频繁的初始化和销毁，从而显著降低了开销。

Buddy Allocation

• 因为合并对分配程序很关键，所以人们设计了一些方法，让合并变得简单，一个好例子就是二分伙伴分配程序（binary buddy allocator）

• 在这种系统中，空闲空间首先从概念上被看成大小为 2^N 的大空间。当有一个内存分配请求时，空闲空间被递归地一分为二，直到刚好可以满足请求的大小（再一分为二就无法满足）。这时，请求的块被返回给用户。

• 在下面的例子中，一个 64KB 大小的空闲空间被切分，以便提供 7KB 的块：

• 在这个例子中，最左边的 8KB 块被分配给用户（如上图中深灰色部分所示）。请注意，这种分配策略只允许分配 2 的整数次幂大小的空闲块，因此会有内部碎片（internal fragment）的麻烦。

• 伙伴系统的漂亮之处在于块被释放时。如果将这个 8KB 的块归还给空闲列表，分配程序会检查“伙伴”8KB 是否空闲。如果是，就合二为一，变成 16KB 的块。然后会检查这个 16KB 块的伙伴是否空闲，如果是，就合并这两块。这个递归合并过程继续上溯，直到合并整个内存区域，或者某一个块的伙伴还没有被释放。

• 伙伴系统运转良好的原因，在于很容易确定某个块的伙伴。怎么找？仔细想想上面例子中的各个块的地址。如果你想得够仔细，就会发现每对互为伙伴的块只有一位不同，正是这一位决定了它们在整个伙伴树中的层次。（2n 和 2n+1，2n 对应的二进制表示最低位肯定为 0，2n+1 该位即为 1）

Other Ideas

• 上面提到的众多方法都有一个重要的问题，缺乏可扩展性（scaling）。具体来说，就是查找列表可能很慢。因此，更先进的分配程序采用更复杂的数据结构来优化这个开销，牺牲简单性来换取性能。例子包括平衡二叉树、伸展树和偏序树。

• 考虑到现代操作系统通常会有多核，同时会运行多线程的程序（本书之后关于并发的章节将会详细介绍），因此人们这了许多工作，提升分配程序在多核系统上的表现。这只是人们为了优化内存分配程序，在长时间内提出的几千种想法中的两种。感兴趣的话可以深入阅读。或者阅读 glibc 分配程序的工作原理，你会更了解现实的情形。

Summary

• 在本章中，我们讨论了最基本的内存分配程序形式。这样的分配程序存在于所有地方，与你编写的每个 C 程序链接，也和管理其自身数据结构的内存的底层操作系统链接。与许多系统一样，在构建这样一个系统时需要这许多折中。对分配程序提供的确切工作负载了解得越多，就越能调整它以更好地处理这种工作负载。在现代计算机系统中，构建一个适用于各种工作负载、快速、空间高效、可扩展的分配程序仍然是一个持续的挑战。